Lesson 2：Dynamic programming problems solved common template

2、Dynamic programming solution set framework

Topics covered

• leetcode 509 Fibonacci series 简单
• leetcode 322 Money Exchange 中等

Dynamic programming problems (Dynamic Programming) should be a headache for many readers, but these problems are also the most skillful and interesting. This full article for dedicating to this algorithm, and the important of dynamic programming is evident.

This article solves several questions:

What is dynamic programming? What are the techniques for solving dynamic programming problems? How to learn dynamic programming?

Learn more solutions for questions will find that the algorithm questions have serveral common tricks, our subsequent dynamic programming series of chapters, are using this article’s problem-solving fixed template, if you remember, solving dynamic programming problems will be a lot easier. So this article is placed in the first chapter, to touch the core of dynamic programming, to summary a set of thinking framework for solving this type of problem, I hope it will become a part of the guidelines for solving dynamic planning problems. In this paper, we will explain the basic set of algorithms framework, the essential or meaningful learning materials is coming.

First of all, the key of the dynamic programming problem is to find the extremum value. Dynamic programming is the most optimization method of Operations Research in fact, but in the region of solving computer problems is more often used, such as make you to find the longest increasing subsequence inside a given seqence, the minimum edit distance between given two string and so on.

What is the core problem of solving dynamic programming? The core problem of solving dynamic programming is exhaustive enumeration. Because of the requirements of the extremum value, we must exhaustive enumeration all feasible answers, and then find the extremum value in it.

Dynamic programming is so simple that it’s just a matter of exhaustion? All the dynamic programming problems I’ve seen are very difficult!

First of all, the exhaustion of dynamic programming is a bit special, because this kind of problem has “overlapping subproblems”, and it will be extremely inefficient if exhaustion is done violently, so you need “memo” or “DP table” to optimize the exhaustion process and avoid unnecessary calculations.

Moreover, a dynamic programming problem must have an “optimal substructure” in order to reach the extremum value of the original problem through the extremum value of the subproblems.

In addition, although the core idea of Dynamic Programming is to exhaustively search for the extremum value, the problem can be so varied that exhaustively searching for all feasible solutions is not an easy task, and the only way to do so is to list out the correct “state transfer equations”.

The above mentioned overlapping subproblems, optimal substructure, and state transfer equations are the three elements of dynamic programming. What do you mean by that? I will give you some examples, but in actual algorithmic problems, it is most difficult to write state transfer equations, which is why many friends find dynamic programming problems difficult. I’ll provide you with a framework of thinking that I have researched and developed to assist you in thinking about state transfer equations:

Define base case -> Define “state” -> Define “choice” -> Define the meaning of dp array/function.

By following the above steps, the final result will be able to apply this framework:

// pseudo-code 
//init base case 
dp[0][0][...] = base case
//do state transfer
for _,state1 = range all_state_values_of_state1{
    for _,state2 = range all_state_values_of_state2{
        for ...{
            dp[state1][state2][...] = extremum(choise1,choise2， ...)
        }
        
    }
} 

Below is a detailed explanation of the fundamentals of dynamic programming through the Fibonacci series problem and the coin change problem. The former is mainly to make you understand what is the overlap of the subproblem (Fibonacci series does not seek the maximum value, so strictly speaking is not a dynamic programming problem), the latter is mainly focused on how to list the transfer of state equations.

I. Fibonacci series

Please don’t mind the simplicity of this example. Only simple examples will allow you to focus fully on the general ideas and techniques behind the algorithm, and not be baffled by the obscure details. If you want difficult examples, there are plenty of them in my history article.

• 1. Violent recursion

The mathematical form of the Fibonacci sequence is recursive, written as code:

func fib(n int) int {
    if n < 2{
        return n
    }
    return fib(n-1)+fib(n-2)
}

This does not need to be said, the school teacher recursion when it seems to take this example. We also know that this writing code is simple and easy to understand, but very inefficient, inefficient in what? Suppose n = 20, please draw the recursive tree:

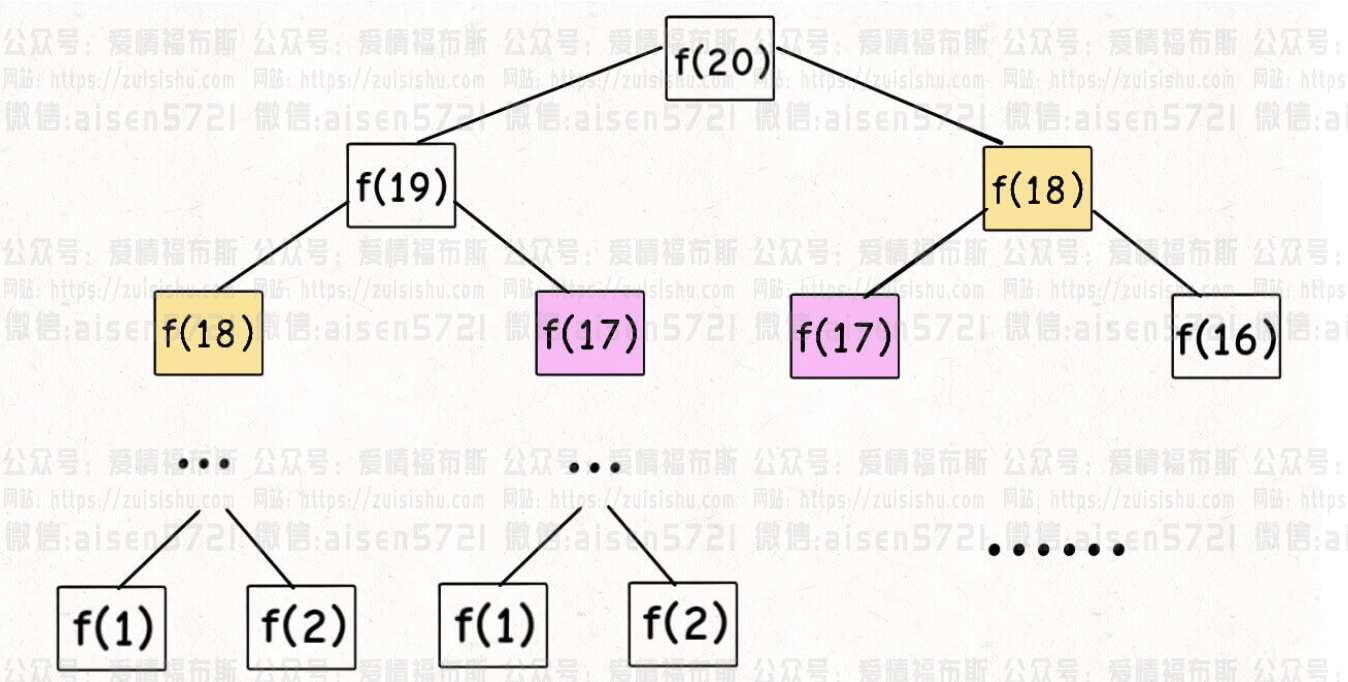
PS: whenever you encounter a problem that requires recursion, it is best to draw a recursion tree, which will help you tremendously in analyzing the complexity of the algorithm and finding the reasons for its inefficiency.

How do we understand this recursive tree? It means that if I want to compute the original problem f(20), I have to compute the subproblems f(19) and f(18), and then if I want to compute f(19), I have to compute the subproblems f(18) and f(17), and so on. When I finally get to f(1) or f(2), the result is known, so I can just return the result, and the recursive tree doesn’t grow any further down.

How do you calculate the time complexity of a recursive algorithm? It is the number of subproblems multiplied by the time it takes to solve a subproblem.

First calculate the number of subproblems, that is, the total number of nodes in the recursive tree. Obviously the total number of nodes in a binary tree is exponential, so the number of subproblems is O(2^n).

Then calculate the time to solve a subproblem, in this algorithm, there is no loop, only f(n - 1) + f(n - 2) an addition operation, the time is O(1).

So, the time complexity of this algorithm is the multiplication of the two, which is O(2^n), exponential level, exploding.

Looking at the recursive tree, it’s obvious why the algorithm is inefficient: there’s a lot of double-counting, e.g., f(18) is counted twice, and as you can see, this recursive tree rooted at f(18) is huge, and counting it more than once would take a huge amount of time. What’s more, f(18) is not the only node that is double-counted, so the algorithm is inefficient.

This is the first property of the dynamic programming problem: the overlapping subproblem. Below, we figure out how to solve this problem.

• 2. Recursive solution with memoization

By clarifying the problem, you have actually solved half of it. That time-consuming reason is repeated calculations, then we can create a “memo”, each time the answer to a sub-problem do not rush to return, the first note to the “memo” and then return; each time a sub-problem first go to the “memo” to check, if you find that the problem has been solved before, directly take out of the answer to use, do not waste time to calculate it again.

Generally use an array as the “memo”, of course, you can also use a hash table (dictionary), the idea is the same.

func fib(n int) int {
    // memo all intialize to 0
    var memo []int = make([]int, n+1)
    // recursive with memo
    return helper(memo,n)
}
func helper(memo []int, n int) int {
    // base case
    if n < 2{
        return n
    }
    // have calculated，no need to calculate a second time 
    if memo[n]!=0{
        return memo[n]
    }
    return helper(memo,n-1) + helper(memo,n-2)
}

Now, draw the recursion tree and you’ll know exactly what the ‘memo’ did.

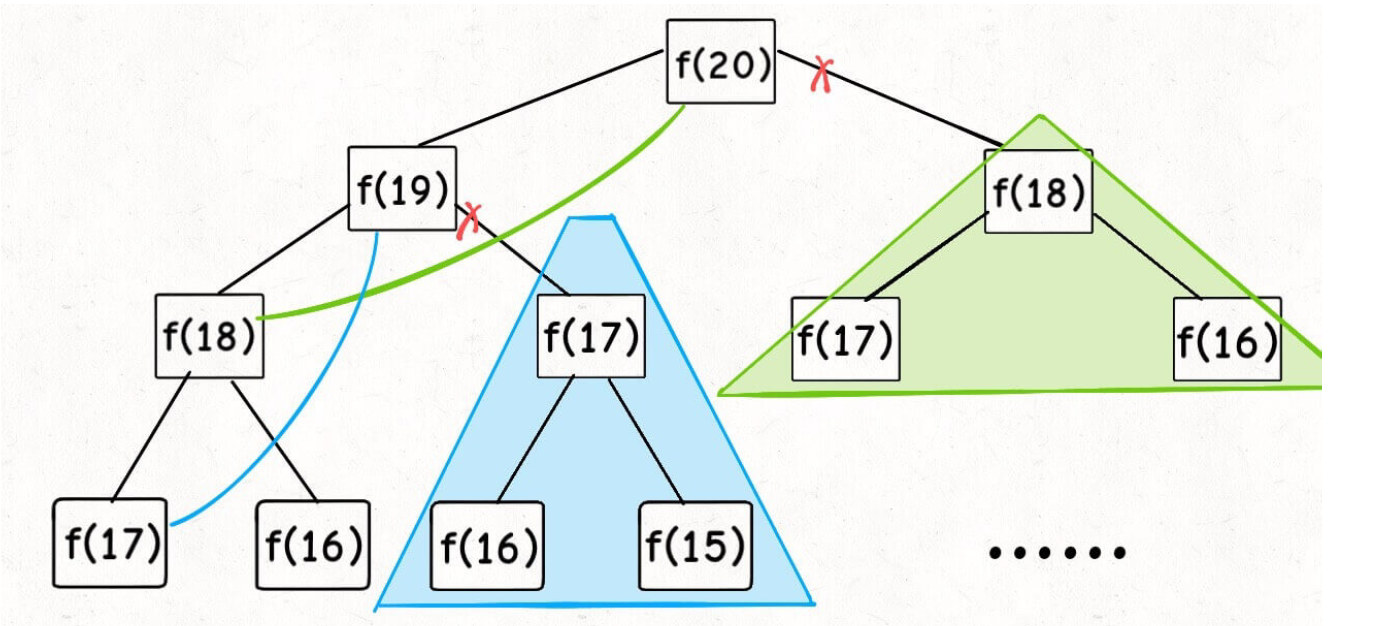
In fact, recursive algorithms with “memoization” transform a recursive tree with huge redundancy into a recursive graph without redundancy by “pruning”, which greatly reduces the number of subproblems (i.e., nodes in the recursive graph).

How is the time complexity of a recursive algorithm calculated? It is the time required to solve a subproblem multiplied by the number of subproblems.

The number of subproblems, i.e., the total number of nodes in the graph, is O(n) since there is no redundant computation in this algorithm, and the subproblems are f(1), f(2), f(3) … f(20), which is proportional to the input size n = 20.

The time to solve a subproblem, ditto, without any loops, is O(1).

So, the time complexity of this algorithm is O(n). It is a dimensionality reduction hit compared to the violent algorithms.

So far, the recursive solution with memoization has been as efficient as the iterative dynamic programming solution. In fact, this solution is almost as efficient as iterative dynamic programming, except that this method is called “top-down” and dynamic programming is called “bottom-up”.

What does “top-down” mean? Note that the recursive tree (or diagram) we just drew is extended from top to bottom, from a larger original problem such as f(20), down gradually decompose the scale, until the base case of f(1) and f(2), and then return the answer layer by layer, which is called “top-down”.

What do you mean by “bottom-up”? In turn, we directly from the bottom, the simplest, the smallest problem size f(1) and f(2) began to push up until we want to push the answer f(20), which is the idea of dynamic planning, which is why dynamic planning are generally out of recursion, but by the cycle of iteration to complete the calculation.

• 3. dp array of iterative solution

With the last step “memo” inspiration, we can take this “memo” independently of a table, called DP table it, in this table to complete the “bottom-up” projection is not beautiful!

func fib(n int) int {
    if n ==0{
        return 0
    }
    var dp []int = make([]int,n+1)
    //base case
    dp[0],dp[1]=0,1
    // state transfer
    for i:=2; i<=n; i++{
        dp[i]=dp[i-1]+dp[i-2]
    }
    return dp[n]
}

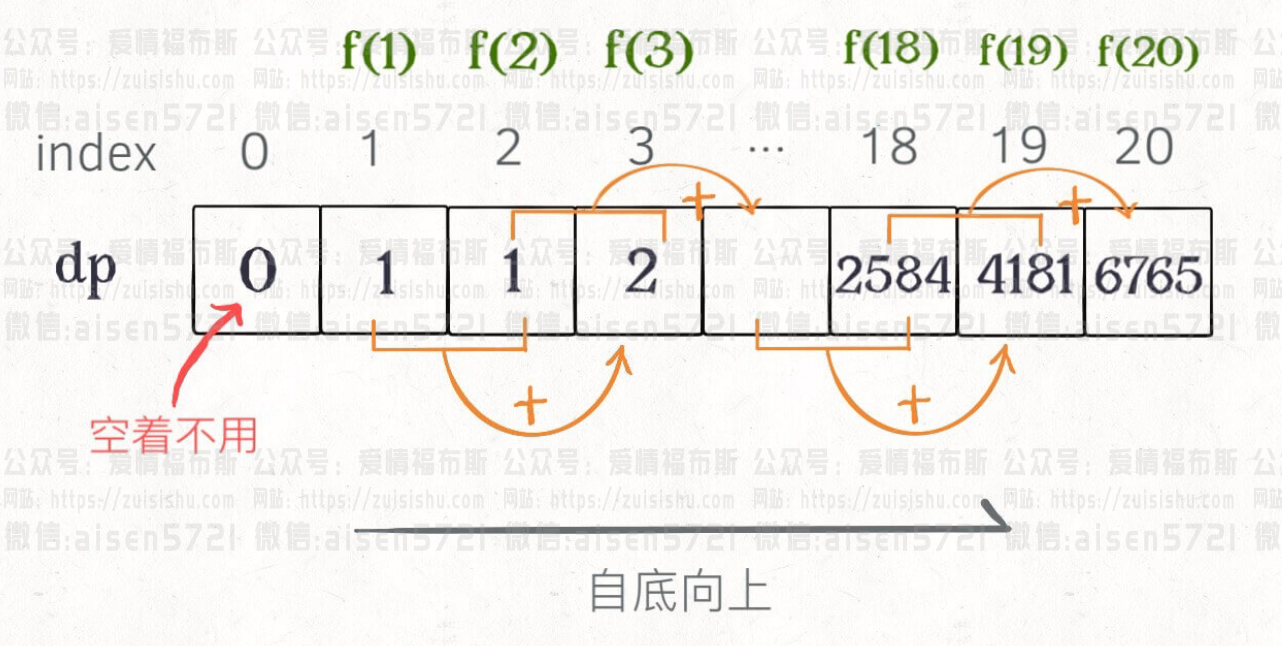
It’s easy to understand when you draw a picture, and you realize that this DP table is especially like the result of the previous one after “pruning”, just counting in reverse. In fact, the “memo” in the recursive solution with memo is this DP table when it is finally completed, so these two solutions are actually similar, and in most cases, the efficiency is basically the same.

Here, the term “state transfer equation” is introduced, which is actually a mathematical type that describes the structure of the problem:

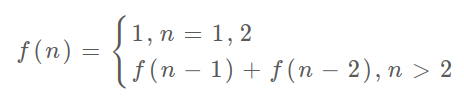
Why is it called the “transfer of state equation”?Well, it’s really just to sound high end. You think of f(n) as a state n, which is transferred from the addition of state n - 1 and state n - 2. This is called a state transfer, and that’s it.

You’ll notice that all of the operations in the above solutions, such as return f(n - 1) + f(n - 2), dp[i] = dp[i - 1] + dp[i - 2], and the initialization operations on memos or DP tables, are all different manifestations of this equation. You can see the important of listing the ‘state transfer equation’, which the core of the problem. And it’s easy to see that the state transfer equation actually directly represents a brute force solution.

Don’t look down on the violent solution, the most difficult part of the dynamic programming problem is to write the violent solution, i.e. the transfer of state equation. As long as the violent solution is written, the optimization method is just a memo or DP table, and there is no more mystery.

This example ends with a detailed optimization. Careful readers will find that, according to the Fibonacci series of state transfer equation, the current state is only related to the previous two states, in fact, it does not need such a long DP table to store all the states, as long as you find a way to store the previous two states on the line. Therefore, it can be further optimized to reduce the space complexity to O(1):

func fib(n int) int {
    if n < 2{
        return n
    }
    //base case
    p,q,r := 0,0,1
    // state transfer
    for i:=2; i<=n; i++{
        p = q
        q = r
        r = p + q
    }
    return r
}

This technique is called “state compression”. If we find that we only need a part of the DP table for each state transfer, then we can try to use state compression to reduce the size of the DP table to record only the necessary data, which is equivalent to reducing the size of the DP table from n to 2. We will also see such an example in the subsequent chapters of Dynamic Programming. The above example is equivalent to reducing the size of the DP table from n to 2. We will see more examples of this in the subsequent chapters on dynamic programming, generally compressing a two-dimensional DP table into a one-dimensional one, i.e., compressing the space complexity from O(n^2) to O(n).

Some people may ask why another important property of dynamic programming, “optimal substructure”, is not covered. It will be covered below. The Fibonacci series example is not strictly considered dynamic programming because it does not involve finding the extremum value. The above is intended to illustrate the elimination of overlapping sub-problems, and to demonstrate the step-by-step process of obtaining the optimal solution. Below, see the second example, the problem of coins change.

Ⅱ. the problem of coins change

First, let’s look at the problem: you are given k kinds of coins with values c1, c2 … ck. ck, the number of coins of each kind is infinite, and then give a total amount, ask you at least need a few coins to make up this amount, if it is not possible to make up, the algorithm returns -1. The function signature of the algorithm is as follows:

// coins contains all available coin value，amount is the final target value
func coinChange(coins []int, amount int) int {
}

Let’s say k = 3, the available values are 1, 2, and 5, and the total amount = 11. Then at least 3 coins are needed to make it, i.e., 11 = 5 + 5 + 1.

How do you think a computer should solve this problem? Obviously, it is to exhaust all possible ways to get the coins, and then find the minimum number of coins needed.

• 1. Violent Recursion

First of all, this problem is a dynamic programming problem because it has an “optimal substructure”. To comply with the “optimal substructure”, the subproblems must be independent of each other. What do you mean by independent of each other? You certainly do not want to see the mathematical proof, I use an intuitive example to explain.

For example, suppose you take an exam and your grades in each subject are independent of each other. Your original problem is to get the highest overall grade on the exam, so your sub-problems are to get the highest grade in language and the highest grade in math …… In order to get the highest grade in each subject, you need to get the highest score on the corresponding multiple-choice question and the highest score on the fill-in-the-blank question in each subject …… The end result, of course, is that you get a perfect score in each class, which is the highest overall grade.

The correct result is obtained: the highest total score is the total score. Because this process is consistent with the optimal substructure, the subproblems “get the highest score in each subject” are independent of each other and do not interfere with each other.

However, if add a condition: your language and math scores will constrain each other, so that a high math score will lower your language score, and vice versa. In that case, obviously the highest total score you can get on the test won’t be up to the total, and you’ll get the wrong result on that thought just now. Because the subproblems are not independent, the language and math scores cannot be simultaneously optimal, so the optimal substructure is destroyed.

Returning to the coins change problem, why is it consistent with the optimal substructure? For example, if you want to find the minimum number of coins for amount = 11 (the original problem), and if you know the minimum number of coins to come up with amount = 10 (the sub-problem), all you need to do is to add one to the answer of the sub-problem (and pick a coin with value of 1) to get the answer of the original problem. Since there is no limit to the number of coins, the subproblems are independent of each other.

So, since we know that this is a dynamic programming problem, we have to think about how to list the correct state transfer equation?

• 1, determine the base case

this is very simple, obviously the target amount amount of 0 when the algorithm returns 0, because no coins are needed to come up with the target amount.

• 2, Determine the “state”, that is, the variables that will change in the original problem and the subproblems.

Since the number of coins is infinite, and the valuex of the coins is also given in the question, only the target amount will keep approaching the base case, so the only “state” is the target amount.

• 3, Determine the “choice”, that is, the behavior that causes the “state” to change.

Why does the target amount change? Because you are choosing coins, and every coin you choose is equivalent to reducing the target amount. So the value of all the coins is your “choice”.

• 4, clear definition of dp function/array.

We are talking about top-down solution, so there will be a recursive dp function, generally speaking, the function’s parameters are the amount of state transfer will change, that is, the above mentioned “state”; function of the return value is the question requires us to calculate the amount. In the case of this question, there is only one state, the “target amount”, and the question asks us to calculate the minimum number of coins needed to make the target amount. So we can define the dp function like this:

Definition of dp(n): input a target amount n, return the minimum number of coins needed to make the target amount n.

Figure out these key points above, the pseudo-code of the solution can be written:

// pseudo-code template
func coinChange(coins []int, amount int)int{
    // definition：if you want to get total amount n，it needed at least dp(coins, n) count coins
    func dp(n int) int{
        // do choice，choose which needed the least coins as the result
        for _,coin = range coins{
            res = min(res, 1+dp(n-coin))
        }
        return res
    }
    //the question's result is represent by dp(amount)
    return dp(amount)
}
func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

According to the pseudo-code, we can get the final answer by adding base case. Obviously, when the target amount is 0, the number of coins needed is 0. When the target amount is less than 0, there is no solution, and -1 is returned:

// this method，submit at leetcode may occured to timeout
func coinChange(coins []int, amount int)int{
    // definition：the final amount n，it needed at least dp(coins, n) amount coins
    func dp(n int) int{
        // do choice，make the least amount coins as the result
        for _,coin = range coins{
            res = min(res, 1+dp(n-coin))
        }
        return res
    }
    //the question make dp(amount) as the final answer
    return dp(amount)
}
func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

PS: here coinChange and dp function have the same signature, so theoretically there is no need to write an extra dp function. But for the convenience of the explanation later, we still write another dp function to realize the main logic.

At this point, the state transfer equation is actually complete, the above algorithm is already a violent solution, and the mathematical form of the above code is the state transfer equation:

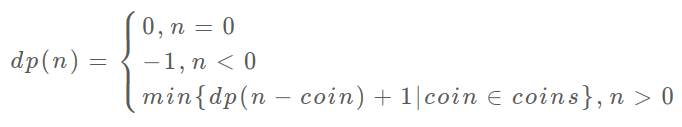
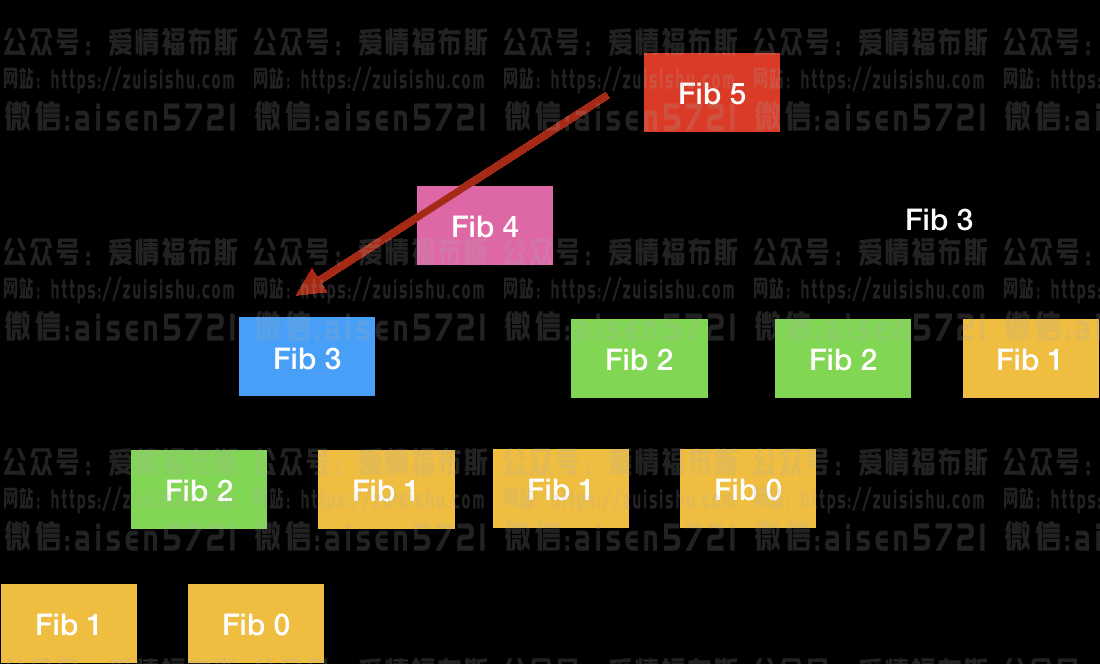
At this point, the problem is actually solved, except that you need to eliminate the overlapping subproblems a bit, e.g., draw the recursive tree when amount = 11, coins = {1,2,5} and see:

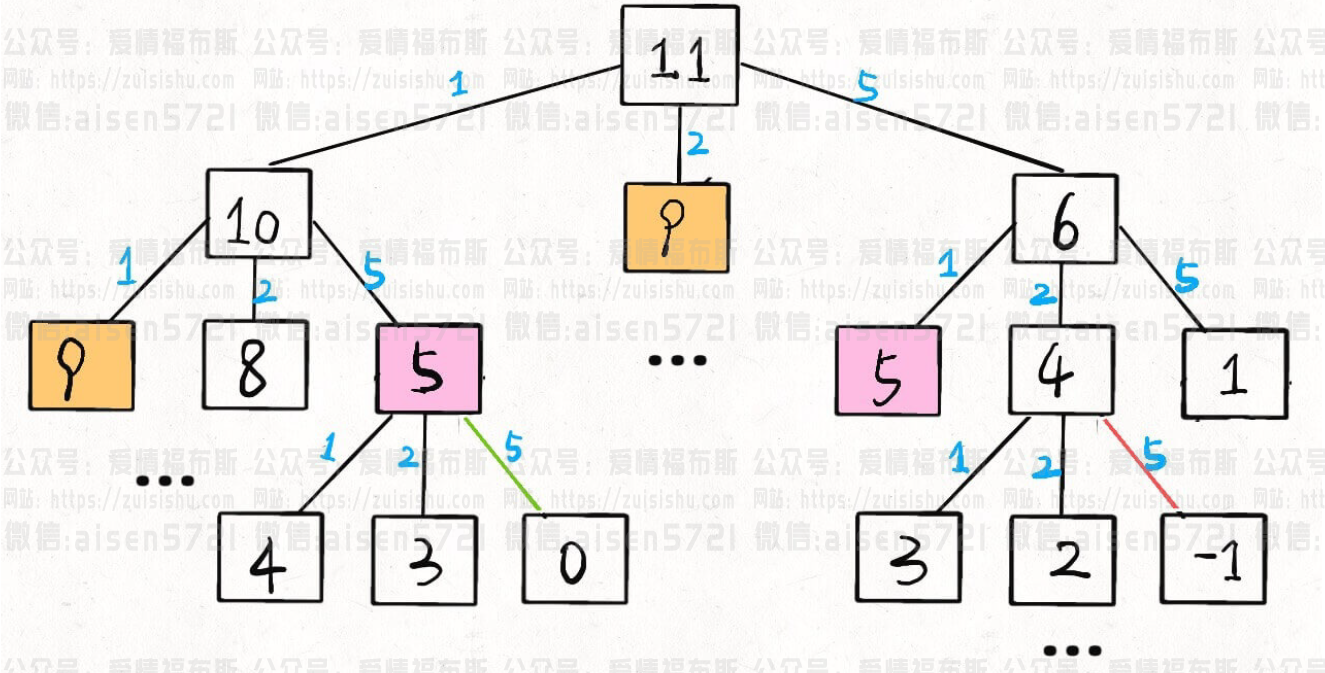
Time complexity analysis of a recursive algorithm: total number of subproblems x time per subproblem.

The total number of subproblems is the number of nodes in the recursive tree, which is harder to see, and is O(n^k), or exponential in any case. Each subproblem contains a for loop, which has a complexity of O(k). So the total time complexity is O(k * n^k), exponential level.

• 2. Recursion with memoization

Similar to the previous example of the Fibonacci series, the subproblems can be eliminated by memoization with only minor modifications:

var memo[]int
func coinChange(coins []int, amount int)int{
    // in golang declare the memo will be intialized to 0
    memo = make([]int, amount + 1)
    //intialized memo
    for i:=0;i<amount+1;i++{
        memo[i]=-666
    }
    return dp(coins,amount)
}
func dp(coins []int, amount int) int{
    if amount ==0 {return 0}
    if amount < 0{return -1}
    // query the memo，forbidden repeat counting
    if memo[amount]!=-666{return memo[amount]}
    res := math.MaxInt32
    for _,coin := range coins{
        // the result of computing sub-problem
        subProblem := dp(coins, amount-coin)
        // no answer for sub-problem，jump over of it
        if subProblem == -1{continue}
        // find the best answer in sub-problems，then plus 1
        res = min(res, subProblem+1)
    }
    // store the computing answer in the memo
    if res == math.MaxInt32{
        memo[amount] = -1
    }else{
        memo[amount] = res
    }
    return memo[amount]
}
func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

Without drawing a diagram, it is clear that ‘memoization’ greatly reduces the number of subproblems and completely eliminates redundancy, so the total number of subproblems does not exceed the number of amounts n, i.e., the number of subproblems is O(n). The time to process a subproblem remains unchanged, still O(k), so the total time complexity is O(kn).

• 3. Iterative solution of dp arrays

Of course, we can also use dp table from the bottom up to eliminate overlapping subproblems, about the “state” “choice” and base case with no difference, the definition of the dp array and the dp function is similar to the definition of the dp function, but also the “state”, that is, the amount of the target as a variable. However, the dp function is reflected in the function parameters, while the dp array is reflected in the array index:

The definition of the dp array: when the target amount is i, at least dp[i] coins are needed.

According to the dynamic programming code framework given at the beginning of our article, the following solution can be written:

func coinChange(coins []int, amount int) int{
    // dp array
    var dp []int = make([]int, amount+1)
    // the array size is amount+1,so intialize it to amount+1
    for i, _ := range dp{
        dp[i] = amount+1
    }
    // base case
    dp[0] = 0
    // outer for loop loop all available state values 
    for i:=1; i<len(dp); i++ { // caution at here because the value geted by using range keyword is unavailable,but indexes can be used,because values geted by using keyword range are unchanged and original array values
        //the goal of inner loop is to get the minium value of all choices
        for _, coin := range coins {
            //no answer for sub-problem,jump over it 
            if i - coin < 0 {
                continue
            }
            dp[i] = min(dp[i], dp[i-coin]+1)
        }
    }
    if dp[amount] == amount + 1{
        return -1
    }else{
        return dp[amount]
    }
}
func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

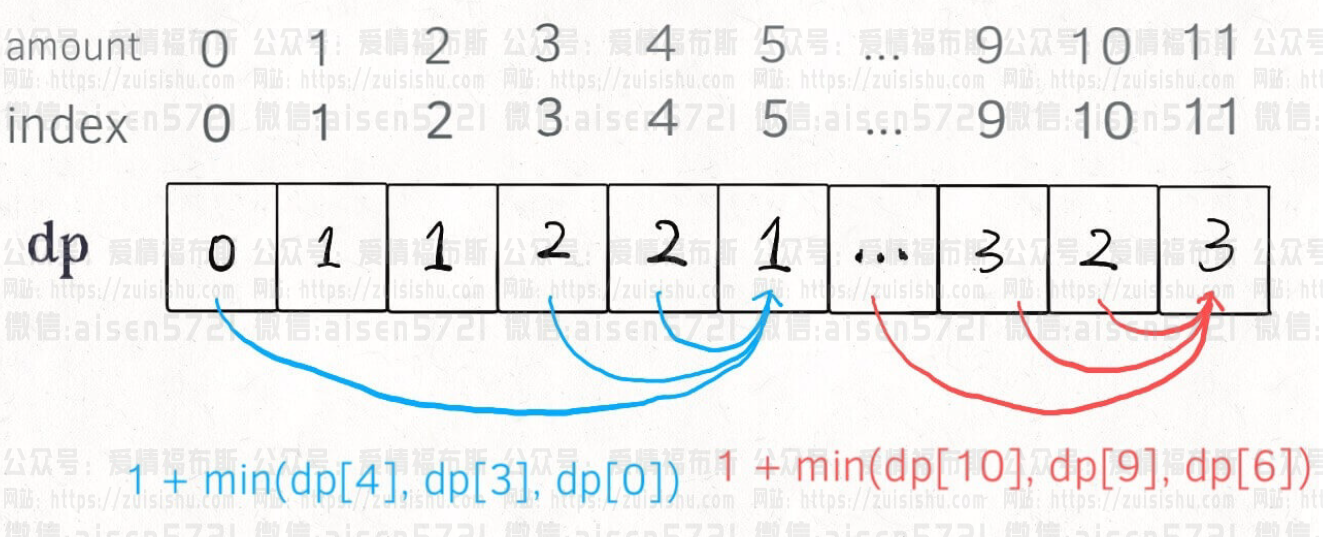
PS: why dp array initialized to amount + 1, because the amount of coins into the sum,only one choice is that the maximum number of coins is equal to the sum (all coins with value of $ 1), so the initialization of the amount + 1 is equivalent to the initialization of the positive infinity, to facilitate the subsequent take the minimum value.Why not directly initialized to the maximum value of int-type Integer.MAX_VALUE it? Because after dp[i - coin] + 1, which will lead to integer overflow.

III. Final Summary

The first Fibonacci series problem explains how to optimize the recursive tree by the ‘memo’ or ‘dp table’ method, and makes it clear that these two methods are essentially the same, just different from top-down and bottom-up.

The second problem of getting change shows how to determine the ’transfer of state equation’ in a procedural way. As long as you write a violent recursive solution via the transfer of state equation, all that’s left to do is to optimize the recursive tree and eliminate the overlapping subproblems.

If you don’t know much about dynamic programming, you should be applauded for reading this, and I’m sure you’ve already mastered this algorithm.

Computers don’t have any tricks to solve problems, their only solution is to exhaust all possibilities. Algorithm design is simply a matter of thinking “how to exhaust” and then pursuing “how to exhaust intelligently”.

list out the state transfer equation is to solve the problem of “how to exhaust”. The reason why it is difficult is that many of the exhaustions need to be realized recursively, and because some of the problems themselves have complex solution spaces that are not so easy to exhaust completely.

Memo, DP table is in pursuit of “how to exhaust intelligently”. The idea of exchanging space for time is the only way to reduce time complexity, otherwise, what else can be played?

After all we will have a chapter dedicated to explain the dynamic programming problem, if you have any questions you can always come back to reread this article, I hope that readers in reading each topic and solution, more to the “state” and “choice” on the leaning, in order to produce your own understanding of this template, and use it freely.